ref : https://www.facebook.com/bhumisiam/posts/1316855285027260
สวัสดีครับแฟนเพจที่รักทุกท่าน
เนื่องจากเมื่อหลายวันก่อนผมได้แนะนำเพื่อนๆ ถึงการเสริมเหล็กในสภาวะสมดุลโดยวิธีหน่วยแรงใช้งานกันไปแล้ว วันนี้ผมจะมาแนะนำการคำนวณการเสริมเหล็กในสภาวะสมดุลโดยวิธีกำลังบ้างนะครับ
ที่ีสภาวะสมดุลนี้ คือ สภาวะที่ความเค้นในเหล็กเสริมต้านทานแรงดึงจะมีค่าเท่ากับค่ากำลังที่จุดคราก (fy) ซึ่งจะมีค่าสูงกว่าค่ากำลังรับแรงดึงในสภาวะที่เราเคยคำนึงถึงก่อนหน้า ซึ่งก็คือ สภาวะหน่วยแรงใช้งาน (fs) และ ความเครียดสูงสุดที่ผิวคานด้านที่เกิดหน่วยแรงอัดให้มีค่าเท่ากับค่าหน่วยความเครียดประลัย มีค่าเท่ากับ 0.003 สาเหตุที่สภาวะนี้เราสมารถใช้ค่าเหล่านี้ ซึ่งเป็นค่าขีดความสามารถสูงสุดของวัสดุได้เป็นเพราะว่า ณ สภาวะนี้เราคำนึงถึงที่สภาวะสูงสุดของการใช้งาน หรือ จะว่าไปเป็นสภาวะที่โครงสร้างกำลังจะเกิดการวิบัตินั่นเอง
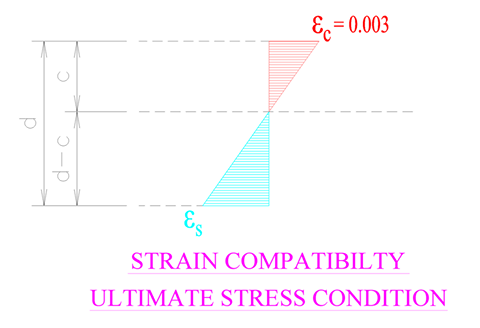
หากเราพิจารณาค่าการกระจายตัวของความเครียดตามในรูปที่ 1 โดยที่เราใช้ความสัมพันธ์ของสามเหลี่ยมคล้ายจะได้ว่า
εs/0.003 = (d-c)/c (1)
โดยหากคูณค่าในเทอมทางซ้ายมือของสมการที่ (1) ด้วยค่าโมดูลัสยืดหยุ่นของเหล็กเสริมเท่ากับ Es สมการที่ (1) จะกลายเป็น
εsEs/0.003Es = (d-c)/c
fy/6120 = (d-c)/c (2)
ดังนั้นหากเราต้องการหาค่าความสัมพันธ์ของระยะด้านบนเหนือแกนสะเทินขึ้นไป หรือระยะ c เราจะสามารถแก้สมการได้ดังนี้
fy / 6120 = (d – c) / c = d / c – c / c = d / c -1
1 + fy / 6120 = d / c
c = d / (1 + fy / 6120) (3)
หากคูณเทอมทางขวามือด้วย 6120/6120 ซึ่งสุดท้ายจะทำให้ค่ามีค่าเท่ากับ 1 จะไม่ส่งผลทำให้ค่าในสมการนี้เปลี่ยนไป เทอมนี้จะเปลี่ยนไปเป็น
c = d / (1 + fy / 6120)(6120 / 6120) = 6120 d / (6120 + fy)
ดังนั้น
c = 6120 d / (6120 + fy) (4)
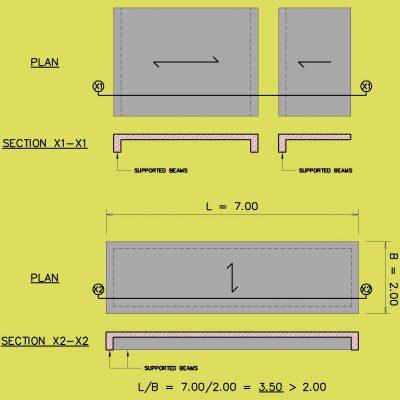
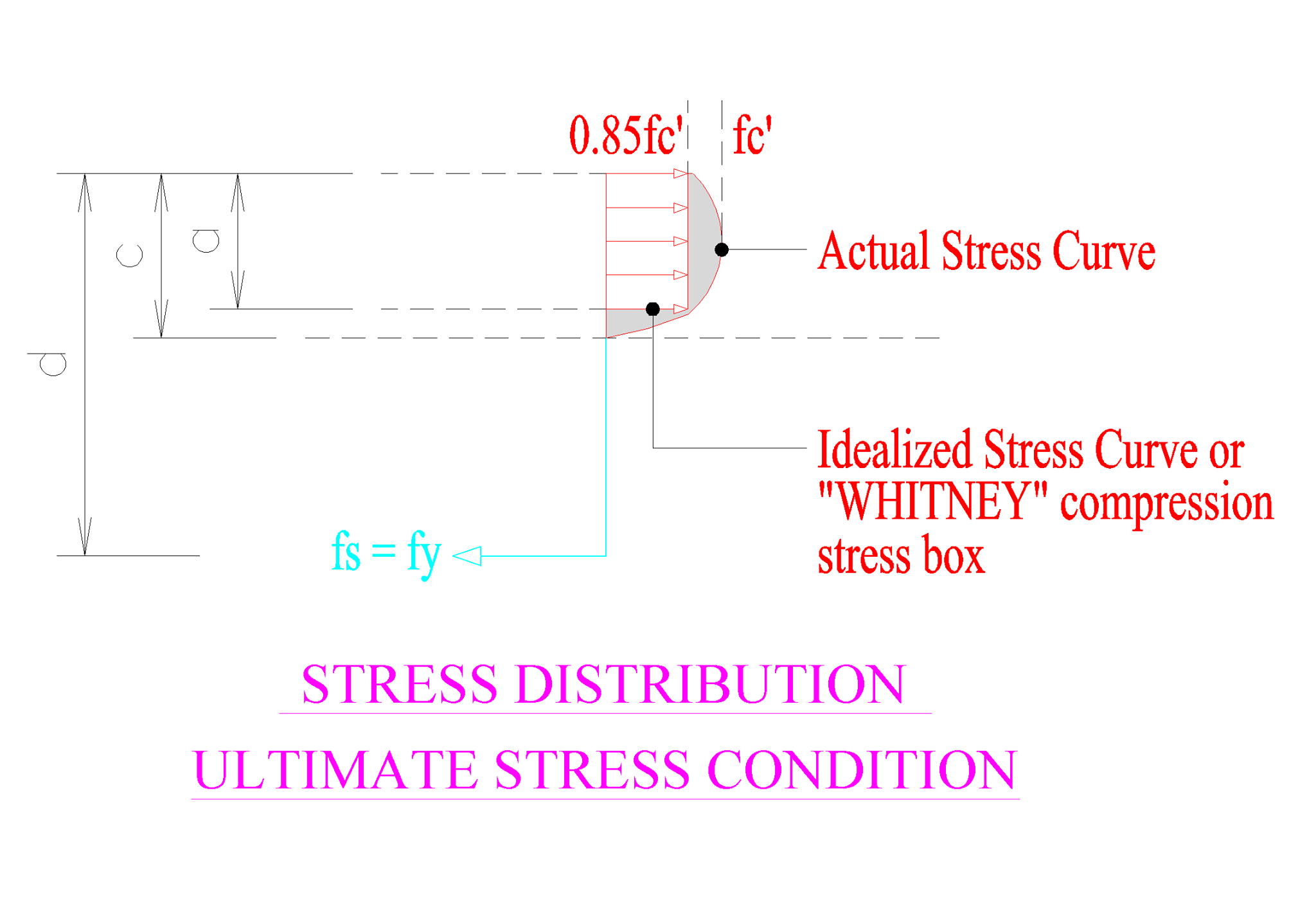
โดยจากในรูปที่ 2 เราจะรู้ว่าค่าความสูงของ WHITNEY COMPRESSION STRESS BOX จะมีค่าเท่ากับระยะ a ซึ่งจะสัมพันธ์กับค่าระยะ c เท่ากับ
a = β1 c
c = a / β1 (5)
แทนค่าสมการที่ (5) ลงใน (4) จะได้
a / β1 = 6120 d / (6120 + fy)
a = 6120 d β1 / (6120 + fy) (6)
จากอีกความสัมพันธ์หนึ่งที่เราทราบดีก็คือ สมดุลระหว่างแรงในหน้าตัดก็คือ แรงดึง ต้องเท่ากับ แรงอัด ดังนั้น
C = T (7)
โดยที่แรงอัดมีค่าเท่ากับ
C = 0.85 fc’ a b (8)
และแรงดึงมีค่าเท่ากับ
T = As fy (9)
และเราทราบว่าค่าความสัมพันธ์ระหว่างหน้าตัดเหล็กเสริมและค่าอัตราส่วนการเสริมเหล็กจะมีค่าเท่ากับ
P = As / b d
As = P b d (10)
แทนค่าสมการที่ (10) ลงใน (9) จะได้ว่า
T = P b d fy (11)
แทนค่าสมการที่ (8) และ (11) ลงในสมการที่ (7) จะได้ว่า
0.85 fc’ a b = P b d fy
P = 0.85 fc’ a b / fy b d = 0.85 fc’ a / fy d (12)
หากเราให้ค่า m เป็นอัตราส่วนระหว่างค่าหน่วยแรงดึงต่อหน่วยแรงอัดจะได้ว่า
m = fy / 0.85 fc’ (13)
แทนค่าสมการที่ (13) ลงใน (12) จะได้ว่า
P = a / m d (14)
แทนค่าสมการที่ (6) ลงใน (4) จะทำให้ทราบว่าค่า P ในที่นี้จะมีค่าเท่ากับ Pb หรือ อัตราส่วนการเสริมเหล็กที่สภาวะสมดุลนั่นเอง หรืออาจสามารถเขียนได้ว่า
P = Pb = [6120 d β1 / (6120 + fy)] / m d
Pb = 6120 β1 / m (6120 + fy) (15)
ดังนั้นการที่ผู้ออกแบบจะมั่นใจได้ว่าสภาวะของโครงสร้างก่อนที่จะเกิดการวิบัตินั้นจะเป็นไปในลักษณะที่ควรจะเป็น หรือ ในลักษณะที่ดี เช่น หากโครงสร้างต้องรับ นน ส่วนเกินไปจากทีไ่ด้รับการออกแบบมากๆ จะมีสัญญาณเตือนภัยเกิดขึ้นในโครงสร้างเรา เป็นต้น เราจึงควรกำหนดให้อัตราส่วนในการเสริมเหล็ก หรือ ค่า Pmax ให้เป็นอัตราส่วนต่อค่า Pb นี้ ซึ่งค่าที่มากที่สุดซึ่ง CODE ยอมให้ใช้ คือ ไม่เกิน 0.75Pb ซึ่งหากต้องการสร้างความมั่นใจให้ยิ่งสูงขึ้นไปอีกสำหรับกรณีงานก่อสร้างบางประเภทที่ไม่อาจวางใจได้ในคุณภาพของงานก่อสร้าง เพื่อนๆ บางท่านอาจเลือกใช้ค่าที่ต่ำกว่าได้ เช่น เท่ากับ 0.5Pb เป็นต้นครับ
ดังนั้นข้อมูลที่ผมนำมาฝากเพื่อนๆ จะทำให้เราทราบแล้วนะครับว่าค่าที่มีความเหมาะสมในการออแบบอัตราส่วนเหล็กเสริมในหน้าตัดของโครงสร้าง คสล เมื่อต้องรับแรงดัดนั้นควรจะต้องทำการคำนึงถึงให้ค่า As req’d ที่หน้าตัดต้องการนั้นมีค่าสูงกว่าค่า As min และน้อยกว่า As max ทั้งนี้เพื่อให้ได้หน้าตัดที่ประหยัดและปลอดภัยต่อการใช้งานสูงสุดนั่นเองครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อยนะครับ จนกว่าจะพบกันใหม่
ADMIN JAMES DEAN
BSP-Bhumisiam
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ
1) สามารถทำงานในที่แคบได้
2) ไม่ก่อให้เกิดมลภาวะทางเสียง
3) หน้างานสะอาด ไม่มีดินโคลน
4) สามารถรับน้ำหนักได้ 20-40 ตัน/ต้น
5) สามารถตอกชิดผนังกำแพง ไม่ทำให้โครงสร้างเดิมเสียหาย
สนใจติดต่อสินค้า เสาเข็ม ไมโครไพล์ (Micropile) สปันไมโครไพล์ (Spun MicroPile) มาตรฐาน มอก. ของ ภูมิสยาม ซัพพลาย ติดต่อ สายด่วน โทร 081-634-6586