ref : https://www.facebook.com/bhumisiam/posts/1315299961849459
สวัสดีครับแฟนเพจที่รักทุกท่าน
วันนี้ผมจะมายก ตย เพิ่มเติมให้แก่เพื่อนๆ ในเรื่อง EQUIVALENT LOAD BALANCING METHOD นะครับ
ก่อนอื่นผมต้องขออธิบายให้แก่เพื่อนๆ ทราบก่อนนะครับว่าหลักการในการหา นน บรรทุกเทียบเท่านั้นจะมีค่าเท่ากับค่าโมเมนต์ดัดของโครงสร้าง และ เราแทนค่าให้มีค่าเท่ากับ แรงอัดในเส้นลวด (P) คูณกับระยะเยื้องศูนย์ (e) นั่นเอง หรือ อาจเขียนได้ง่ายๆ ว่า
M = P e (a)
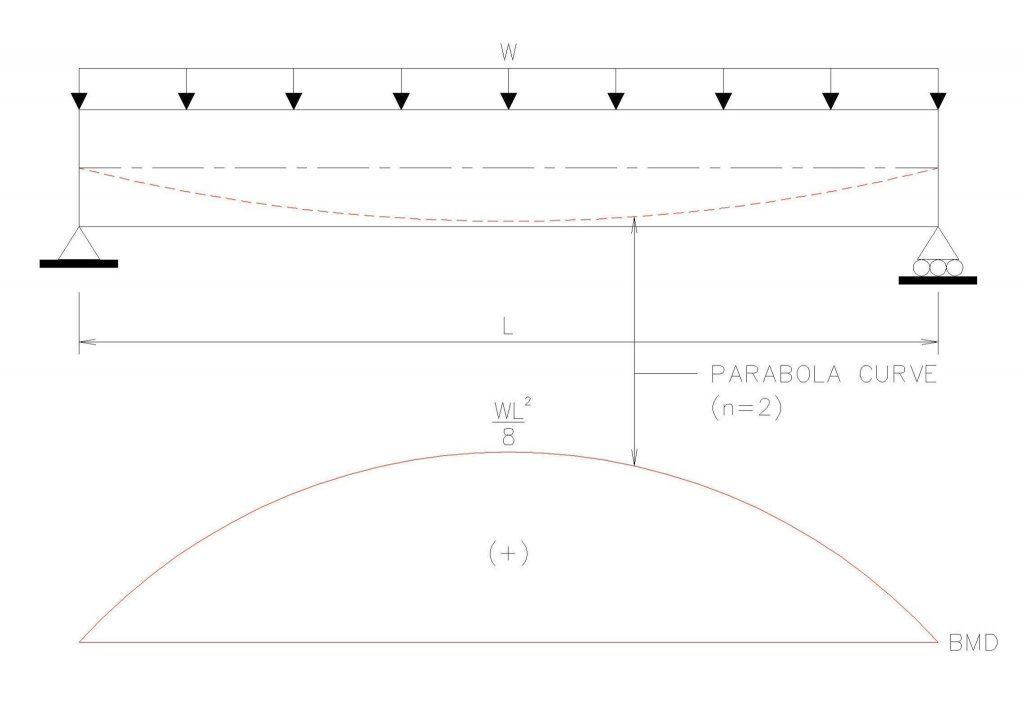
ดังนั้นสำหรับการหาค่า นน บรรทุกเทียบเท่าเมื่อโครงสร้างรับแรงดัด คอร ต้องรับ นน บรรทุกแบบแผ่กระจายสม่ำเสมอ (W หรือ UNIFORMLY DISTRIBUTED LOAD) ก็คือเท่ากับ
M = W L^(2) / 8 (b)
หากแทนสมการที่ (a) ให้เท่ากับ (b) จะได้ว่า
W L^(2) / 8 = P e (c)
ดังนั้นค่า W balance จะมีค่าเท่ากับการแก้สมการที่ (c) ได้ว่า
W = W balance = 8 P e / L^(2) (d)
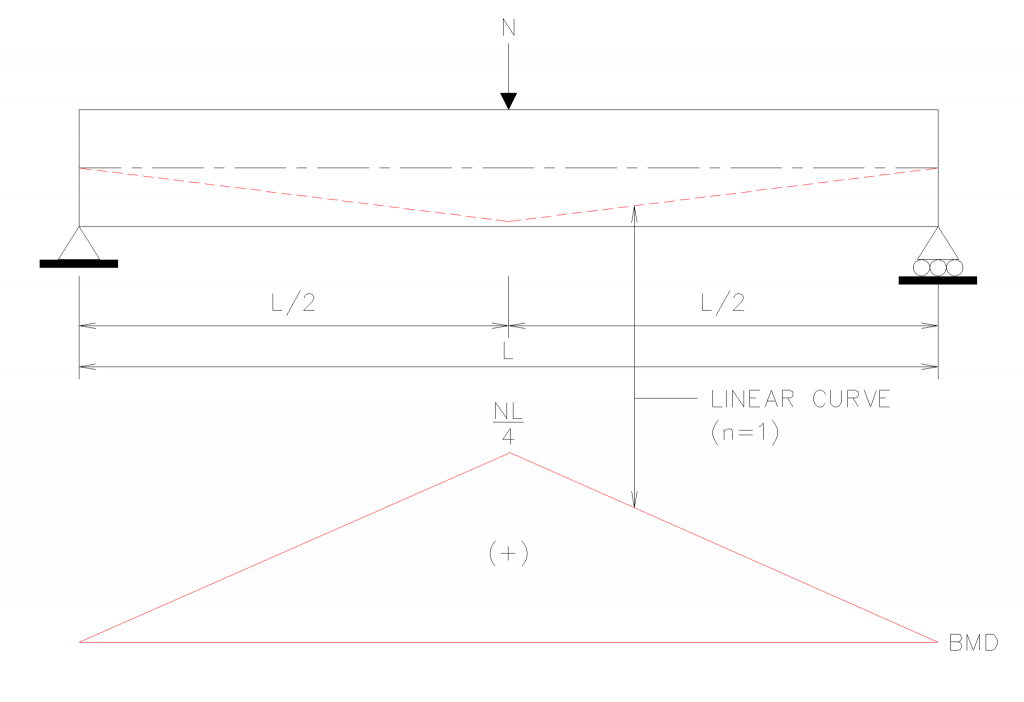
ส่วนการหาค่า นน บรรทุกเทียบเท่าเมื่อโครงสร้างรับแรงดัด คอร ต้องรับ นน บรรทุกแบบเป็นจุด (N หรือ CONCENTRATED LOAD) ก็คือเท่ากับ
M = N L / 4 (e)
หากแทนสมการที่ (a) ให้เท่ากับ (e) จะได้ว่า
N L / 4 = P e (f)
ดังนั้นค่า N balance จะมีค่าเท่ากับการแก้สมการที่ (g) ได้ว่า
N = N balance = 4 P e / L (g)
มาถึง ตย กันบ้างนะครับ ตย ข้อนี้เป็นการประยุกต์มาจากการสถานการณ์ในการทำงานจริงๆ นั่นเองครับ คือ เมื่อโครงสร้างรับแรงดัด คอร ต้องรับ นน บรรทุกแบบแผ่กระจายสม่ำเสมอ (W) และ นน แบบเป็นจุด (N) ร่วมกัน เช่น ในการออกแบบแผ่นพื้น คอร ที่ต้องรับ นน ทั้งสองแบบ แต่ การวางแนวเส้นลวดจำเป็นต้องวางให้เป็นเส้นโค้ง หรือ ไม่สามารถวางให้แนวของลวดเป้นเส้นตรงให้สอดคล้องตรงตามทฤษฎีได้นั่นเองครับ
หากเพื่อนๆ จะต้องเจอกับเหตุการณ์แบบนี้ เพื่อนๆ มีแนวความคิดในการแก้ปัญหาในลักษณะแบบนี้อย่างไรครับ ?
งงกับคำถามหรือไม่ครับ ?
งั้นผมขออนุญาตใบ้ให้นิดหนึ่งนะครับ เพื่อนๆ คิดว่าเราควรทำการ
(1) รวมผลของ นน เทียบเท่าและแทนค่าหาแรงในเส้นลวด หรือ
(2) รวมผลค่าโมเมนต์เทียบเท่าแล้วค่อยแทนค่าหาแรงในเส้นลวด
คอนเซปต์ไหนถึงจะให้คำตอบในการออกแบบที่ดีครับ ?
เรามาดูคำตอบกันดีกว่านะครับ เอาคอนเซปต์แรกก่อนละกัน จาก (a) เราจะทราบว่า
Mb = P e (1)
และยังทราบอีกว่า
Mb = Wb L^(2)/8 (2)
และจากคอนเซปต์นี้นะครับ เราให้ว่า
Balance Load = Total Load
Wb = Wt = W + N/L (3)
แทนค่าให้สมการที่ (1) = (2)
P e = Wb L^(2)/8 (4)
แทนค่าในสมการที่ (3) ลงในสมการที่ (4) จะได้แรงอัดในเส้นลวดต้องมีค่าเท่ากับ
P = (W + N/L)L^(2)/8e
โดยหากให้ค่า L^(2)/8e เท่ากับ γ จะได้ว่า
P = (W + N/L) γ (5)
เรามาดูคอนเซปต์ที่สองต่อนะกัน เราจะทราบว่าหากให้สมการที่ (1) = (2) จะได้ว่า
Wb = 8 P e / L^(2) (6)
และจากคอนเซปต์นี้นะครับ เราให้ว่า
Balance Moment = Total Moment (7)
ดังนั้น
Mb = WL^(2)/8 + NL/4 (8)
และ
Mt = (Wt)L^(2)/8 (9)
จากหลักการที่กล่าวถึงในสมการที่ (7) เราให้สมการที่ (8) เท่ากับ (9)
WL^(2)/8 + NL/4 = (Wt)L^(2)/8
Wt = 8/L^(2) [ WL^(2)/8 + NL/4 ]
Wt = W + 2N/L (10)
จากหลักการที่กล่าวถึงในสมการที่ (7) เราให้สมการที่ (1) เท่ากับ (9)
P e = (Wt)L^(2)/8
P = (Wt)L^(2)/8e (11)
แทนค่าสมการที่ (10) ลงใน (11) จะได้แรงอัดในเส้นลวดต้องมีค่าเท่ากับ
P = (W + 2N/L)L^(2)/8e
โดยหากให้ค่า L^(2)/8e เท่ากับ γ จะได้ว่า
P = (W + 2N/L) γ (12)
โดยหากเปรียบเทียบคำตอบในสมการที่ (5) และ (12) จะพบว่าคำตอบในสมการที่ (12) จะให้ค่าแรงอัดในเส้นลวดที่มีค่าสูงกว่านั่นเอง เหตุที่ออกมาเป็นเช่นนี้ก็ง่ายๆ ตรงไปตรงมาครับ เพราะ เนื่องจากการแปลง นน บรรทุกแบบจุดให้เป็น นน บรรทุกแบบแผ่กระจายสม่ำเสมอนั้นสามารถทำได้ครับ แต่ สิ่งสำคัญกว่านั้น คือ หากวิเคราะห์โครงสร้างแล้วจะพบว่าค่าโมเมนต์ดัดที่ได้นั้นจะไม่เทียบเท่ากันนั่นเอง
ดังนั้นเมื่อเพื่อนๆ ต้องออกแบบ นน บรรทุกในลักษณะแบบนี้ก็อย่าลืมคำนึงถึงผลข้อนี้ในการออกแบบด้วยนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากเพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อยนะครับ จนกว่าจะพบกันใหม่
ADMIN JAMES DEAN
BSP-Bhumisiam
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ
1) สามารถทำงานในที่แคบได้
2) ไม่ก่อให้เกิดมลภาวะทางเสียง
3) หน้างานสะอาด ไม่มีดินโคลน
4) สามารถรับน้ำหนักได้ 20-40 ตัน/ต้น
5) สามารถตอกชิดผนังกำแพง ไม่ทำให้โครงสร้างเดิมเสียหาย
สนใจติดต่อสินค้า เสาเข็ม ไมโครไพล์ (Micropile) สปันไมโครไพล์ (Spun MicroPile) มาตรฐาน มอก. ของ ภูมิสยาม ซัพพลาย ติดต่อ สายด่วน โทร 081-634-6586
http://www.micro-pile.com