สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
ในทุกๆ วันศุกร์ (แห่งชาติ) แบบนี้ ผมก็จะมาพบกับเพื่อนๆ เพื่อที่จะได้มาพูดคุยและเสวนากันถึงหัวข้อ “ฝากคำถาม-เราจะมาตอบให้” นะครับ
สืบเนื่องมาจากเมื่อวันอังคารที่ผ่านมาซึ่งผมได้ทำการอธิบายถึงเรื่อง การแก้ไขโครงสร้างฐานรากที่ใช้เสาเข็มโดยการเพิ่มจำนวนของโครงสร้างเสาเข็มเข้าไป ซึ่งผมได้อธิบายไว้ว่า หลักการที่ง่ายที่สุดในการเพิ่มคือ ให้ทำการเพิ่มจำนวนของเสาเข็มให้อยู่ตรงกันกับตำแหน่งของจุดศูนย์ถ่วงของโครงสร้างฐานราก หรือ หากทำเช่นนั้นไม่ได้ก็ให้ทำการตรวจสอบว่าตำแหน่งในการโครงสร้างเสาเข็มนั้นทำให้จุดศูนย์ถ่วงของกลุ่มโครงสร้างเสาเข็มให้ตรงกันกับตำแหน่งของจุดศูนย์ถ่วงของโครงสร้างฐานรากน่ะครับ
ซึ่งในวันนั้นผมเองก็ได้ให้คำแนะนำกับเพื่อนๆ ไว้ด้วยว่า สมการในการตรวจสอบตำแหน่งของจุดศูนย์ถ่วงของกลุ่มโครงสร้างเสาเข็มนั้นก็คือสมการ
Yb = ∑Ai×yi / ∑Ai
ซึ่งสมการข้างต้นเป็นสมการพื้นฐานที่เพื่อนๆ แฟนเพจที่เป็นวิศวกรน่าที่จะคุ้นเคยกันดีอยู่แล้วเพราะเราต้องใช้สมการๆ นี้ในการคำนวณหลายๆ เรื่องเลย เช่น ในการคำนวณทางด้านกลศาสตร์ของโครงสร้าง หรือ STRUCTURAL MECHANICS หรือ ในการคำนวณทางด้านงานออกแบบโครงสร้างคอนกรีตเสริมเหล็ก หรือ RC STRUCTURAL DESIGN เป็นต้น แต่ทั้งนี้เพื่อเป็นการทบทวนความจำแก่เพื่อนๆ วันนี้ผมจึงจะขออนุญาตมาทวนและยกตัวอย่างถึงวิธีการใช้งานสมการๆ นี้ให้ก็แล้วกันนะครับ
ค่า Yb ก็คือ ตำแหน่งของจุดศูนย์ถ่วงของโครงสร้างที่เรากำลังพิจารณา โดยที่ค่าๆ นี้จะอยู่ในทางทิศทางใด ก็จะขึ้นอยู่กับตำแหน่งที่เราใช้ในการอ้างอิงเป็นหลัก ค่า Ai ก็คือ ขนาดของพื้นที่หน้าตัดของชิ้นส่วนโครงสร้างที่เรากำลังพิจารณา และ ค่า yi ก็คือ ตำแหน่งของชิ้นส่วนโครงสร้างที่เรากำลังพิจารณา โดยที่ค่าๆ นี้จะอยู่ในทางทิศทางใด ก็จะขึ้นอยู่กับตำแหน่งที่เราใช้ในการอ้างอิงเป็นหลัก ซึ่งผมต้องขอเน้นไว้ตรงนี้เลยว่า จากสมการๆ นี้จะสามารถใช้ได้สำหรับกรณีที่ชิ้นส่วนโครงสร้างนั้นมีความแข็งแรงของวัสดุที่เท่าๆ กันเท่านั้น เอาละเพื่อเป็นการไม่เสียเวลา เรามาดูตัวอย่างง่ายๆ ประกอบคำอธิบายของผมเลยก็แล้วกันนะครับ
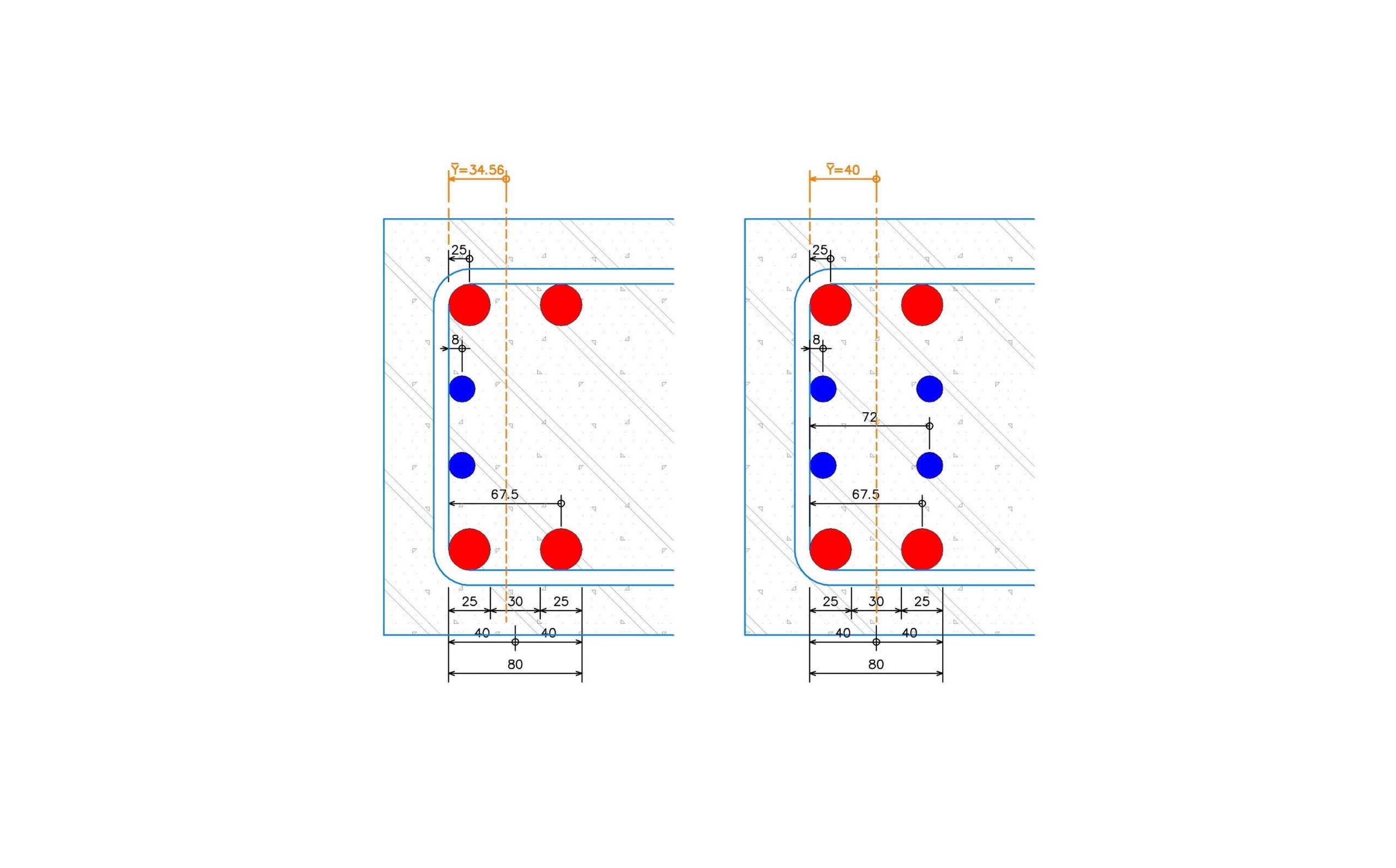
ผมทำตัวอย่างขึ้นมา 2 ตัวอย่าง โดยที่เป็นตัวอย่างของการจัดเหล็กเสริมในหน้าตัดโครงสร้างคาน คสล รับแรงดัด โดยที่ในกรณีที่ 1 จะเป็นการวางเหล็กเสริมแบบสมมาตร ซึ่งพอผลจากการคำนวณออกมาเพื่อนๆ ก็จะเห็นได้ว่าตำแหน่งของจุดศูนย์ถ่วงของกลุ่มเหล็กเสริมนั้นจะอยู่ที่ตรงกึ่งกลางแบบพอดิบพอดีเลย สำหรับกรณีที่ 2 จะเป็นการวางเหล็กเสริมแบบไม่สมมาตร ซึ่งพอผลจากการคำนวณออกมาเพื่อนๆ ก็จะเห็นได้ว่าตำแหน่งของจุดศูนย์ถ่วงของกลุ่มเหล็กเสริมนั้นจะไม่ได้อยู่ที่ตรงกึ่งกลางเหมือนในกรณีที่ 1 แล้วน่ะครับ
เรามาเริ่มต้นจากกรณีที่ 1 ก่อนก็แล้วกัน ซึ่งผมจะทำการคำนวณหาค่า Ai ก่อน ซึ่งสำหรับกรณีนี้จะมีค่า Ai ทั้งหมด 2 ค่า นั่นก็คือ A1 สำหรับเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 16 มม ซึ่งจะมีค่าเท่ากับ 2.01 ตร.ซม และ A2 สำหรับเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 25 มม ซึ่งจะมีค่าเท่ากับ 4.91 ตร.ซม นะครับ
ค่าต่อมาก็คือ yi บ้าง ซึ่งสำหรับกรณีนี้จะมีค่า yi ทั้งหมด 4 ค่านั่นก็คือ สำหรับเหล็กในแถวบน 2 ค่า และเหล็กในแถวล่างอีก 2 ค่า ผมจะเริ่มจากเหล็กแถวล่างก่อนนะ นั่นก็คือ สำหรับเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 16 มม ซึ่งจะมีค่าเท่ากับ 8 มม และสำหรับเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 25 มม ซึ่งจะมีค่าเท่ากับ 12.5 มม ต่อมาก็คือ เหล็กแถวบน นั่นก็คือ สำหรับเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 16 มม ซึ่งจะมีค่าเท่ากับ 72 มม และสำหรับเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 25 มม ซึ่งจะมีค่าเท่ากับ 67.5 มม ดังนั้นหากเราทำการแทนค่าต่างๆ ที่หาเอาไว้ข้างต้นเราก็จะสามารถทำการคำนวณหาค่า Yb สำหรับกรณีที่ 1 ออกมาได้มีค่าเท่ากับ
Yb = [ ( 2×2.01×8 + 2×4.91×12.5 ) + ( 2×2.01×72 + 2×4.91×67.5 ) ] / ( 4×2.01 + 4×4.91 )
Yb = 1107.2 / 27.68
Yb = 40 มม
เรามาต่อกันที่กรณีที่ 2 เลยนะ สำหรับกรณีนี้จะมีค่า Ai ทั้งหมด 2 ค่า เหมือนเดิม และจะมีความแตกต่างออกไปจากกรณีที่ 1 ตรงที่ค่า yi ซึ่งจะไม่มีค่า yi สำหรับเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 16 มม ดังนั้นหากเราทำการแทนค่าต่างๆ ที่หาเอาไว้ข้างต้นเราก็จะสามารถทำการคำนวณหาค่า Yb สำหรับกรณีที่ 2 ออกมาได้มีค่าเท่ากับ
Yb = [ ( 2×2.01×8 + 2×4.91×12.5 ) + ( 2×4.91×67.5 ) ] / ( 2×2.01 + 4×4.91 )
Yb = 817.76 / 23.66
Yb = 34.56 มม
ซึ่งเพื่อนๆ จะเห็นได้ว่า ผลจากการคำนวณจากกรณที่ 1 จะพบว่าตำแหน่งของจุดศูนย์ถ่วงของกลุ่มเหล็กเสริมนั้นจะอยู่ที่ตรงกึ่งกลางแบบพอดิบพอดีเลยและสำหรับกรณีที่ 2 ที่ตำแหน่งของจุดศูนย์ถ่วงของกลุ่มเหล็กเสริมนั้นจะอยู่ค่อนลงมาต่ำกว่าตำแหน่งกึ่งกลางเล็กน้อยนั้นก็เป็นเพราะว่า ที่เหล็กเสริมแถวบนนั้นจะขาดหายไปซึ่งเหล็กข้ออ้อยขนาดเส้นผ่าศูนย์กลาง 16 มม ซึ่งจะส่งผลทำให้ตำแหน่งของจุดศูนย์ถ่วงของชิ้นส่วนโครงสร้างนั้นลดต่ำลงมาเล็กน้อยนั่นเองครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านจากคำถามในวันนี้น่าที่จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์วันศุกร์
#ฝากคำถามแล้วเราจะมาตอบให้
#เทคนิคในการคำนวณหาระยะจุดศูนย์ถ่วงของชิ้นส่วนโครงสร้างที่มีความแข็งแรงเทียบเท่ากัน
ADMIN JAMES DEAN
Bhumisiam (ภูมิสยาม)
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปันไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service)
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม เสาเข็มสปันไมโครไพล์ Spun Micro Pile และเสาเข็มไอไมโครไพล์ I Micropile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐานเสาเข็มคอนกรีตเสริมเหล็กแบบแรงเหวี่ยง มอก.397-2562 และมาตรฐานเสาเข็มคอนกรีตเสริมเหล็กอัดแรงหล่อสำเร็จ มอก.396-2549 การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน ทดสอบการรับน้ำหนักโดยวิธี Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
สอบถามเพิ่มเติมได้ 24ชม. ทุกวันค่ะ
☎️ 082-790-1447
☎️ 082-790-1448
☎️ 082-790-1449
☎️ 091-9478-945
☎️ 091-8954-269
☎️ 091-8989-561
📲 https://lin.ee/hum1ua2
📥 https://m.me/bhumisiam










