ตัวอย่างและเฉลยข้อสอบในวิชา THEORY OF STRUCTURES
เฉลย
สิ่งที่เราควรทำเมื่อเจอปัญหาแบบนี้ คือ เราควรที่จะต้องมองให้ออกเสียก่อนว่าโครงสร้างนั้นๆ จะสามารถที่จะทำการวิเคราะห์โครงสร้างได้โดยวิธี อย่างง่าย หรือ อย่างยาก ในปัญหาข้อนี้ก็เช่นกัน หากเราทำการตรวจสอบหาค่าดัชนีของความยากในการวิเคราะห์ (DEGREE OF DETERMINACY) หากเราให้ค่า EQ.EQ. คือ จำนวนของสมการสมดุล (EQUILIBRIUM EQUATIONS) ค่า C คือ จำนวนของจุดต่อภายใน (INTERNAL HINGED) และ ค่า R คือ จำนวนของแรงปฏิกิริยาที่จุดรองรับ
เราจะพบว่าเรามีค่าแรงที่เราทราบค่า (KNOWN DATA) อยู่ทั้งหมดเท่ากับ
EQ.EQ. + C = 3 + 0 = 3
และเรามีค่าแรงที่เราไม่ทราบค่า (UNKNOWN FORCES) อยู่ทั้งหมดเท่ากับ
R = 3
ซึ่งค่าดัชนีของความยากในการวิเคราะห์สามารถที่จะหาได้จากการที่เรานำ ค่าแรงที่เราไม่ทราบค่า ลบกันกับ ค่าแรงที่เราทราบค่า ซึ่งจะมีค่าเท่ากับ ศูนย์ นั่นเอง ดังนั้นปัญหาข้อนี้เราจึงสามารถที่จะทำการวิเคราะห์ได้ด้วยวิธีการ อย่างง่าย เพราะฉะนั้นเราก็สามารถที่จะอาศัยสมการสมดุลในการวิเคราะห์โครงสร้างได้โดยที่ไม่จำเป็นต้องอาศัยวิธีการใดๆ ที่มีความยุ่งยากเลย
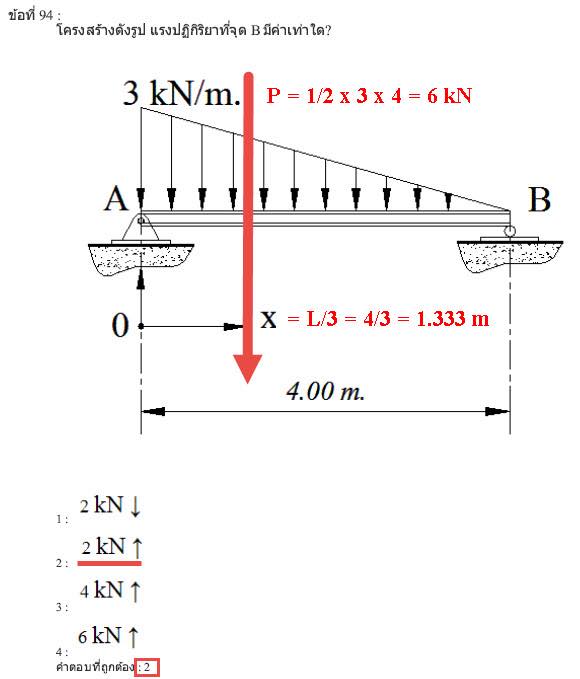
ดังนั้นในเมื่อเราต้องการที่จะทราบค่าแรงปฏิกิริยาที่จุด B เราก็จะทำการ TAKE MOMENT รอบจุด A เพียงแต่ว่าลักษณะพิเศษอีกอย่างหนึ่งของปัญหาข้อนี้ คือ รูปแบบของแรงกระจายตัวจะเป็นแรงกระทำในแนวดิ่งแบบไม่คงที่ หรือ ที่เราเรียกกันว่า แรงกระจายตัวแบบเชิงเส้น (LINEAR DISTRIBUTED LOAD)
ซึ่งจริงๆ แล้วหลักในการวิเคราะห์โครงสร้างที่มีแรงลักษณะแบบนี้อยู่ก็ไม่ได้มีความยากเย็นอะไรเป็นพิเศษนะครับ เรายังคงสามารถที่จะใช้หลักการพื้นฐานของการ TAKE MOMENT ทั่วๆ ไปได้ นั่นก็คือ แรง คูณกันกับ ระยะทาง ซึ่งผมเชื่อว่าในพจน์ของ แรง เพื่อนๆ ไม่น่าจะมีปัญหาในการวิเคราะห์ค่าๆ นี้ ก็จะทำให้เหลือพจน์ ระยะทาง เท่านั้น
ระยะทางในที่นี้จะไม่ใช่ตำแหน่งกึ่งกลางของแรง แต่ จะเป็นที่ตำแหน่งจุดศูนย์ถ่วงของแรง ซึ่งเราทราบดีว่าจุดศูนย์ถ่วงสำหรับแรงกระทำที่เป็นรูปสามเหลี่ยมจะอยู่ที่ ระยะทาง ส่วน สาม จากด้านยอดของสามเหลี่ยม ซึ่งสำหรับปัญหาข้อนี้ คือ 4/3 = 1.333 M จากด้านยอดของสามเหลี่ยม เพียงเท่านี้เราก็จะสามารถที่จะนำหลักการ TAKE MOMENT ไปใช้ในการวิเคราะห์โครงสร้างได้แล้วนะครับ
∑M@A = 0 (COUNTER CLOCKWISE DIRECTION IS +)
4V@B – (½)(3)(4)(1.333) = 0
4V@B – 8 = 0
4V@B = +8
V@B = +8/4
V@B = +2 kN (↑)
ดังนั้นคำตอบในข้อนี้ คือ ข้อที่ 2 เท่ากับ 2 kN ในทิศทาง ขึ้น
ข้อคิดท้ายเฉลย
ข้อสอบข้อนี้มีความต้องการที่จะทดสอบดูว่า วิศวกร ที่เป็นผู้มาทำข้อสอบข้อนี้จะมี ไหวพริบ และ ความรู้ เกี่ยวกับ ระบบของโครงสร้าง หรือ ลักษณะของแรงต่างๆ มาก หรือ น้อย เพียงใด
ข้อแนะนำท้ายเฉลย
หากผมจะให้คำแนะนำในการทำข้อสอบข้อนี้ ผมคิดว่าน้องๆ ไม่ควรที่จะเสียเวลาสำหรับคำถามข้อนี้มากกว่า 5 นาทีนะครับ มิเช่นนั้นอาจจะทำข้อสอบโดยรวมทั้งหมดไม่ทันได้นะครับ
ยังไงผมก็ขอเป็นกำลังใจให้น้องๆ วิศวกรทุกๆ คนที่กำลังเตรียมตัวที่จะสอบใบประกอบวิชาชีพทุกๆ คนด้วยนะครับ และ หากน้องๆ ท่านใดมีคำถามเกี่ยวกับข้อสอบใบประกอบวิชาชีพที่อาจจะยัง ติดขัด หรือ อาจจะไม่ทราบถึงหลักในการคำนวณ ผมก็ขอรบกวนให้ทำการแจ้งเข้ามาที่เพจได้เลยนะครับ ผมจะค่อยๆ ทำการทยอยนำมาเฉลยและตอบให้แก่น้องๆ ทุกๆ คนต่อไปครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN
Bhumisiam ภูมิสยาม
ผู้ผลิตรายแรก Spun MicroPile
(1) ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐาน ISO 9001:2015
(2) ได้รับมาตรฐาน ISO 9001:2015 UKAS ภายใต้การดูแลของ อังกฤษ
(3) ได้รับมาตรฐาน ISO 9001:2015 NAC ภายใต้การดูแลของ สมอ.
(4) ได้รับมาตรฐาน มอก. 397-2524 เสาเข็ม Spun MicroPile Dia 21, 25, 30 cm.
(5) ผู้ผลิต Spun MicroPile ที่ได้รับ Endorsed Brand รับรองคุณภาพมาตรฐานจาก SCG
(6) ผู้นำระบบ Computer ที่ทันสมัยผลิต เสาเข็ม Spun MicroPile
(7) ลิขสิทธิ์เสาเข็ม Spun MicroPile
(8) เทคโนโลยีการผลิต จากประเทศเยอรมัน
(9) ผู้ผลิต Spun MicroPile แบบ “สี่เหลี่ยม”
(10) การผลิตคอนกรีตและส่วนผสม ใช้ Program SCG-CPAC
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ
(1) สามารถทำงานในที่แคบได้
(2) ไม่ก่อให้เกิดมลภาวะทางเสียง
(3) หน้างานสะอาด ไม่มีดินโคลน
(4) สามารถรับน้ำหนักได้ 20-50 ตัน/ต้น ขึ้นอยู่กับสภาพชั้นดินแต่ละพื้นที่
(5) สามารถตอกชิดกำแพง ไม่ก่อให้โครงสร้างเดิมเสียหาย
สนใจติดต่อสินค้า เสาเข็มสปันไมโครไพล์ มาตรฐาน มอก. โทร
063-889-7987
082-790-1447
082-790-1448
082-790-1449
http://www.spun-micropile.com
http://www.micro-pile.com
http://เสาเข็มสปันไมโครไพล์.com











